Soliton gas describes a statistical ensemble of solitons in integrable wave systems, arising from the balance between dispersion and nonlinearity. It models wave turbulence in nonlinear media, offering insights into soliton interactions and collective behavior across optics, Bose-Einstein condensates, and fluid dynamics.
1.1 Definition and Concept
A soliton gas refers to a statistical ensemble of solitons, which are localized, stable waveforms that maintain their shape during propagation. In the context of the nonlinear Schrödinger equation (NLSE), soliton gas arises as a large collection of interacting solitons. These solitons are characterized by their particle-like behavior, balancing dispersion and nonlinearity. The concept involves describing solitons as discrete structures within a continuous wave field, enabling the study of their collective dynamics. Soliton gas is mathematically defined through the inverse scattering transform, which associates solitons with discrete eigenvalues of the Zakharov-Shabat operator. This framework allows for the analysis of soliton interactions and their statistical properties, making soliton gas a powerful tool for understanding wave turbulence in integrable systems. It finds applications in Bose-Einstein condensates, nonlinear optics, and deep-water waves, where soliton ensembles model complex wave behavior.
1.2 Relevance in Nonlinear Wave Systems
Soliton gas plays a pivotal role in understanding nonlinear wave systems, particularly in modeling wave turbulence and soliton interactions. It provides a statistical framework to describe large ensembles of solitons, enabling the analysis of their collective behavior in integrable systems. The nonlinear Schrödinger equation (NLSE) is central to these studies, as it governs wave propagation in various media, such as optical fibers, Bose-Einstein condensates, and deep-water waves. Soliton gas bridges the gap between individual soliton dynamics and macroscopic wave phenomena, offering insights into modulation instability and the emergence of coherent structures in turbulent systems. This concept is instrumental in predicting and controlling wave behavior in diverse physical contexts, from nonlinear optics to fluid dynamics, making it a cornerstone of modern wave theory and its applications.
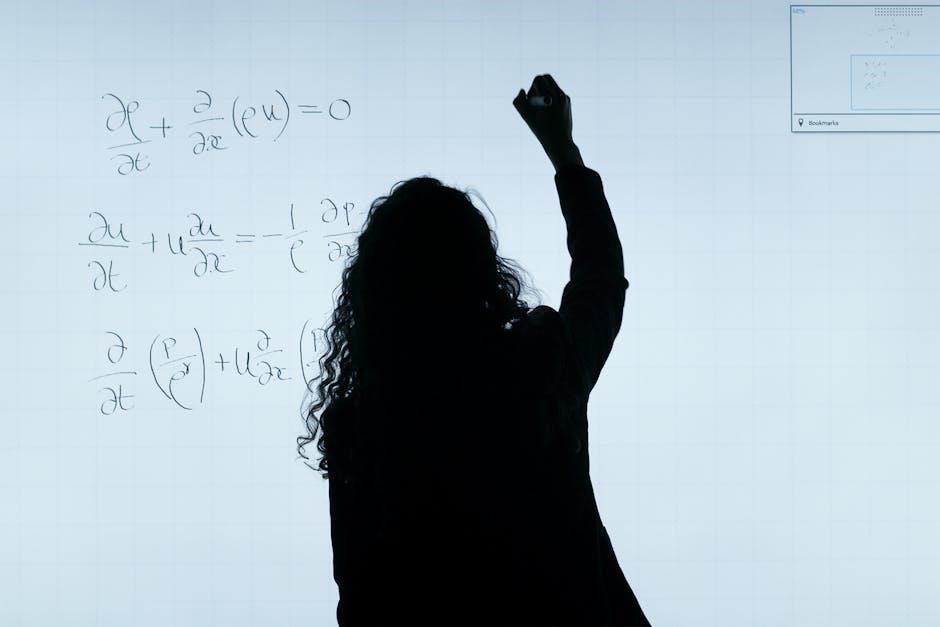
The Nonlinear Schrödinger Equation (NLSE)
The NLSE is a fundamental equation describing wave propagation in nonlinear media, balancing dispersion and self-interaction. It governs phenomena in optics, BEC, and water waves.
2.1 Mathematical Formulation
The Nonlinear Schrödinger Equation (NLSE) is a fundamental partial differential equation describing wave propagation in nonlinear media. Mathematically, it is expressed as:
iψ_t + ψ_xx + 2|ψ|²ψ = 0,
where ψ(x, t) is a complex wave function, x and t are space and time variables, and the subscripts denote partial derivatives. The equation captures the balance between dispersion (ψ_xx) and self-focusing/defocusing nonlinearity (2|ψ|²ψ). The focusing case (positive coefficient) supports bright solitons, while the defocusing case (negative coefficient) supports dark solitons. The NLSE is integrable, meaning it possesses an infinite number of conserved quantities, enabling exact soliton solutions. Its Lax pair formulation, involving compatibility conditions between two linear systems, underpins its integrability and soliton dynamics.
2.2 Focusing NLSE and Soliton Formation
The focusing Nonlinear Schrödinger Equation (NLSE) is a special case where the nonlinearity enhances the intensity of the wave, leading to the formation of stable, localized soliton solutions. Solitons in the focusing NLSE are characterized by their balance between dispersion and self-focusing effects, resulting in wave packets that maintain their shape and velocity during propagation. The inverse scattering transform method is a powerful tool for constructing soliton solutions, revealing that solitons are associated with discrete eigenvalues in the scattering spectrum. For the focusing NLSE, bright solitons emerge as sech-shaped profiles, while dark solitons, characterized by phase jumps, arise in defocusing media. The soliton gas concept extends this to large ensembles of solitons, modeling their statistical behavior in integrable wave systems. This formulation underpins soliton dynamics in nonlinear optics, Bose-Einstein condensates, and deep-water waves.

Soliton Gas: A Statistical Ensemble
Soliton gas represents a statistical ensemble of solitons, describing large collections of interacting solitons in integrable wave systems. It provides a framework for understanding collective soliton behavior and emergent wave turbulence phenomena in nonlinear media.
3.1 Inverse Scattering Transform Approach
The inverse scattering transform (IST) method is a powerful tool for solving integrable nonlinear partial differential equations, such as the nonlinear Schrödinger equation (NLSE). This approach involves associating the NLSE with a scattering problem, where the potential is related to the wave function. By solving the direct scattering problem, one obtains spectral data, which can then be inverted to reconstruct the solution. For soliton gas, the IST method is used to analyze the scattering data of a system with an infinite number of solitons. This allows for the derivation of soliton solutions and their statistical properties. The method is particularly useful for studying soliton interactions and their collective behavior in large ensembles. IST provides a rigorous mathematical framework for understanding soliton gas dynamics in various physical systems, including Bose-Einstein condensates and nonlinear optics.
3.2 Statistical Description of Solitons
A statistical description of solitons in soliton gas involves analyzing the distribution and interactions of a large number of soliton solutions. This approach treats solitons as particles in a gas, characterized by their density, velocity, and interactions. The statistical ensemble is constructed by considering the scattering data, such as the number of solitons, their spectral parameters, and the separation between them. This method is essential for understanding the collective behavior of solitons in integrable systems, including their distribution in phase space and their contribution to the overall dynamics. The statistical description provides a macroscopic view of soliton gas, enabling the study of phenomena like soliton density fluctuations and the emergence of universal patterns in soliton interactions. This approach bridges the gap between microscopic soliton properties and macroscopic system behavior, offering insights into wave turbulence and nonlinear wave dynamics in various physical contexts.

Properties of Soliton Solutions
Soliton solutions are localized, stable waveforms that maintain their shape due to a balance between dispersion and nonlinearity. They exhibit unique properties like soliton interactions and persistence in integrable systems, providing analytical solutions to nonlinear wave equations.

4.1 Bright Solitons
Bright solitons are stable, localized solutions of the focusing nonlinear Schrödinger equation (NLSE), characterized by a hyperbolic secant (sech) profile. They exist in systems with attractive nonlinearity, where dispersion is balanced by self-focusing effects, ensuring the wave packet maintains its shape during propagation. These solitons have positive energy and are mathematically described by parameters such as amplitude, width, and velocity, which determine their interaction dynamics. Bright solitons are fundamental in nonlinear optics, representing optical pulses that resist dispersion, and in Bose-Einstein condensates (BECs), where they model matter waves. Their stability and robustness make them a cornerstone in soliton gas theory, enabling the study of collective behavior in integrable systems. The analytical solutions for bright solitons are derived using methods like the inverse scattering transform, providing a deep understanding of their properties and applications in experimental physics.
4.2 Dark Solitons
Dark solitons are solutions to the defocusing nonlinear Schrödinger equation (NLSE), characterized by a localized dip in intensity against a continuous background. Unlike bright solitons, they arise in systems with repulsive nonlinearity, where self-defocusing effects dominate. Mathematically, dark solitons are described by hyperbolic tangent (tanh) profiles, representing density depressions that propagate without dispersion. These solitons are stable but less robust than their bright counterparts, often requiring specific initial conditions. Dark solitons are relevant in optical fibers, Bose-Einstein condensates, and fluid dynamics, where they model wave phenomena like density holes. Their velocity and shape are determined by parameters such as amplitude and width, with interactions governed by the defocusing nature of the NLSE. Despite their localized nature, dark solitons decay at infinity, distinguishing them from bright solitons in soliton gas dynamics.
4.3 Lattice Solitons
Lattice solitons are stable, localized wave solutions that arise in periodic potentials, such as optical lattices or Bose-Einstein condensates in trapped atomic gases; These solitons are supported by the interplay between nonlinearity and the periodic modulation of the potential. Unlike bright and dark solitons, lattice solitons exist due to the discrete nature of the medium, where the periodic structure allows for the formation of robust, spatially localized states. They are characterized by their ability to propagate without spreading, maintaining their shape over long distances. Lattice solitons are of significant interest in nonlinear optics and quantum physics, offering insights into wave localization in structured media. Their properties, such as stability and mobility, make them valuable for applications in optical communication systems and quantum information processing. Recent studies have explored their dynamics in both theoretical models and experimental setups, highlighting their versatility in soliton gas systems.

Applications of Soliton Gas
Soliton gas has applications in nonlinear optics, Bose-Einstein condensates, and deep-water surface gravity waves, offering insights into wave turbulence and potential advancements in technological systems.
5.1 Bose-Einstein Condensates (BEC)
Soliton gas plays a significant role in the study of Bose-Einstein condensates (BECs), where it describes the behavior of bright solitons in ultracold atomic gases. BECs, being macroscopic quantum systems, provide an ideal platform for observing soliton dynamics. The focusing nonlinear Schrödinger equation (NLSE) governs the formation of bright solitons in BECs with attractive interactions. These solitons are stable, self-reinforcing wave packets that maintain their shape due to the balance between dispersion and nonlinearity. Soliton gas, as a statistical ensemble of such solitons, emerges when multiple solitons interact within the condensate. This concept is crucial for understanding collective behavior in BECs, such as soliton collisions and density distributions. Experimental observations of soliton gas in BECs have confirmed theoretical predictions, highlighting the importance of this framework in quantum fluid dynamics and cold atom physics.
5.2 Nonlinear Optics
In nonlinear optics, soliton gas provides a framework for understanding the propagation of light in nonlinear media, particularly in optical fibers. The nonlinear Schrödinger equation (NLSE) is central to modeling soliton formation in such systems. Soliton gas describes the statistical behavior of large ensembles of optical solitons, which are stable, localized wave packets that balance dispersion and self-phase modulation. These solitons are critical in long-distance optical communication, as they maintain signal integrity over thousands of kilometers. The concept of soliton gas is particularly relevant in systems with high soliton densities, where interactions between solitons become significant. This framework has enabled the development of advanced optical communication technologies, including wavelength division multiplexing (WDM) and soliton-based transmission systems. Experimental validations of soliton gas dynamics in nonlinear optical fibers have further solidified its importance in understanding complex wave phenomena in optics.
5.3 Deep-Water Surface Gravity Waves
The nonlinear Schrödinger equation (NLSE) is instrumental in modeling deep-water surface gravity waves, where soliton gas concepts describe the statistical behavior of wave ensembles. Solitons in this context represent localized wave packets that maintain their shape due to a balance between dispersion and nonlinear effects. In deep-water environments, soliton gas provides a framework for understanding the dynamics of rogue waves and complex wave interactions. Experimental studies have successfully synthesized soliton gas in controlled wave tank settings, validating theoretical predictions. These findings have implications for oceanography, as they offer insights into wave turbulence and energy transfer in natural wave systems. The connection between soliton gas and rogue wave phenomena highlights the importance of this framework in predicting and mitigating extreme wave events in maritime environments. This research bridges theoretical nonlinear wave dynamics with practical applications in oceanography and coastal engineering.

Derivation of Soliton Solutions
Soliton solutions are derived using Darboux transformations, Hirota bilinear method, and Adomian decomposition, providing exact and stable solutions for the nonlinear Schrödinger equation and related systems.
6.1 Darboux Transformations
Darboux transformations are a powerful tool for generating soliton solutions of the nonlinear Schrödinger equation (NLSE). These transformations act on the Lax pair of the equation, modifying the potential while preserving the integrability of the system. By applying Darboux transformations, one can construct explicit formulas for soliton solutions, starting from a seed solution. This method is particularly useful for deriving multi-soliton solutions, where each soliton corresponds to a discrete eigenvalue in the scattering data. The iterative nature of Darboux transformations allows for the generation of solutions with multiple solitons, enabling the study of their interactions. This approach is widely used in the analysis of integrable systems, providing a systematic way to explore the rich variety of soliton solutions in nonlinear wave equations.
6.2 Hirota Bilinear Method
The Hirota bilinear method is a systematic approach to solving integrable nonlinear equations, including the nonlinear Schrödinger equation (NLSE). It involves rewriting the equation in a bilinear form using auxiliary functions, which simplifies the identification of soliton solutions. This method leverages the properties of integrable systems and factorizes the solutions into products of elementary functions, enabling the derivation of soliton solutions through a straightforward algebraic process; The Hirota method is particularly effective for constructing multi-soliton solutions and analyzing their interactions. By transforming the NLSE into a bilinear form, it bypasses the complexities of traditional methods, providing a clear pathway to soliton solutions. This technique has been widely applied to various integrable systems, making it a cornerstone in soliton research and nonlinear wave analysis.
6.3 Adomian Decomposition Method
The Adomian Decomposition Method (ADM) is a powerful analytical technique for solving nonlinear partial differential equations, including the nonlinear Schrödinger equation (NLSE). By decomposing the solution into a series of components, ADM simplifies the handling of nonlinear terms. This method does not require perturbation or linearization, making it suitable for solving complex soliton-related problems. ADM iteratively constructs the solution by solving a sequence of simpler equations derived from the original NLSE. It is particularly effective for obtaining soliton solutions, as it avoids the need for small parameters and provides a direct route to analytical results. The method has been successfully applied to various integrable systems, offering insights into soliton dynamics and their interactions. Its simplicity and accuracy make it a valuable tool in soliton gas research and nonlinear wave analysis.
Modulation Instability (MI) and Soliton Formation
Modulation instability (MI) triggers the emergence of solitons in nonlinear wave systems. It occurs when a stable wave becomes unstable, leading to localized soliton pulses through dispersion-nonlinear balance.
7.1 Critical Parameter Analysis
Critical parameter analysis for modulation instability (MI) reveals thresholds where soliton formation occurs. For the nonlinear Schrödinger equation (NLSE), the critical parameter κ determines instability onset. When κ exceeds a specific value, typically κ > 2, the system becomes unstable, leading to soliton generation. This threshold depends on the balance between dispersion and nonlinearity. At κ = 2, the solution transitions, exhibiting either collapse or blowup in density profiles, influenced by initial conditions like q₀, the center of the initial density. Numerical studies show that above this critical value, solitons emerge as stable, localized structures. This analysis is fundamental for understanding MI-driven soliton formation in nonlinear wave systems, such as optical fibers or Bose-Einstein condensates. The critical parameter defines the boundary between stable wave propagation and soliton gas dynamics, governed by the NLSE.

Statistical Properties of Soliton Gas
Soliton gas exhibits unique statistical properties, including soliton density, distribution, and interaction dynamics. These properties describe the collective behavior of solitons in large ensembles, governed by NLSE.
8.1 Soliton Density and Distribution
The soliton density and distribution within a soliton gas are critical for understanding its statistical behavior. Research indicates that soliton density refers to the number of solitons per unit length or volume, while distribution describes their spatial arrangement. In the context of the nonlinear Schrödinger equation (NLSE), solitons can form dense ensembles where their interactions significantly influence the overall gas dynamics. Studies have shown that in certain regimes, solitons can exhibit clustering behavior, leading to non-uniform distributions. These properties are essential for modeling phenomena like wave turbulence and soliton interactions in integrable systems. The statistical analysis of soliton density and distribution provides insights into the collective behavior of solitons, which is crucial for applications in nonlinear optics and Bose-Einstein condensates.
8.2 Velocity Distribution of Solitons
The velocity distribution of solitons in a soliton gas is a key aspect of their statistical description. Solitons, being localized wave packets, propagate with specific velocities determined by their parameters, such as amplitude and wave number. In the context of the nonlinear Schrödinger equation (NLSE), the velocity of a soliton is typically proportional to its momentum, which is influenced by the balance between dispersion and nonlinearity. The distribution of velocities within a soliton gas can vary depending on the initial conditions and the nature of soliton interactions; For example, in a focusing NLSE, solitons with higher amplitudes generally move faster than those with lower amplitudes. Statistical studies reveal that soliton velocities often follow a specific probability distribution, which is crucial for understanding the gas’s thermodynamic-like behavior. This distribution plays a significant role in modeling wave turbulence and soliton dynamics in integrable systems.
8.3 Interactions in Soliton Gas
Interactions in soliton gas are fundamental to understanding the collective behavior of solitons in integrable wave systems. Solitons, despite their stability, interact with each other through elastic collisions, preserving their shapes and velocities but inducing phase shifts. These interactions are governed by the nonlinear Schrödinger equation (NLSE) and are studied using methods like the inverse scattering transform. The phase shifts depend on soliton parameters, such as amplitude and velocity, and are critical in determining the statistical properties of the gas. Analytical methods, including Darboux transformations, provide insights into multi-soliton solutions, revealing how interactions affect the overall dynamics. Such studies are essential for modeling soliton turbulence and understanding the emergent behavior of soliton ensembles in nonlinear media. These interactions also have implications for applications in optics, Bose-Einstein condensates, and fluid dynamics.

Recent Advances in Soliton Gas Research
Recent studies explore deterministic soliton gas analysis and experimental synthesis in water waves, advancing understanding of soliton interactions and statistical behavior in integrable wave systems.
9.1 Deterministic Soliton Gas Analysis
Deterministic soliton gas analysis focuses on rigorous mathematical approaches to study soliton ensembles with well-defined initial conditions. This method contrasts with stochastic or thermodynamic descriptions, emphasizing precise control over soliton interactions and statistics. Recent advancements utilize the inverse scattering transform (IST) to derive exact solutions for large numbers of solitons, enabling detailed studies of their behavior in integrable systems. For instance, researchers have successfully analyzed ensembles of up to 32 strongly interacting solitons, solving the inverse scattering problem for high numbers of discrete eigenvalues. This deterministic approach provides insights into the collective dynamics of soliton gases, particularly in the context of deep-water surface gravity waves and quantum droplets. By examining specific configurations, scientists can uncover universal patterns in soliton interactions, bridging theoretical models with experimental observations in nonlinear wave systems.
9.2 Experimental Synthesis in Water Waves
Recent experiments have achieved the controlled synthesis of dense soliton gases in deep-water surface gravity waves, marking a significant milestone in nonlinear wave dynamics. By employing advanced techniques such as nonlinear spectral shaping, researchers have successfully generated and observed large ensembles of interacting solitons under controlled laboratory conditions. These experiments validate theoretical models of soliton gas formation and provide insights into wave turbulence in natural systems. The results demonstrate the transition from discrete soliton interactions to a continuous statistical distribution, characteristic of soliton gas. This work not only advances the understanding of soliton dynamics in hydrodynamic systems but also opens new avenues for studying wave turbulence in other nonlinear media, such as nonlinear optics and Bose-Einstein condensates. Experimental synthesis of soliton gases bridges the gap between theoretical predictions and real-world observations.

Interdisciplinary Connections
Soliton gas connects integrable systems, quantum droplets, and nonlinear optics, bridging soliton dynamics across diverse fields, from Bose-Einstein condensates to deep-water surface gravity waves and optical systems.
10.1 Integrable Systems and Solitons
Integrable systems, such as the Nonlinear Schrödinger Equation (NLSE), are characterized by their exact soliton solutions, which maintain stability through dispersion and nonlinearity balance. These systems, including KdV and AKNS equations, enable precise mathematical descriptions of soliton behavior. The inverse scattering transform and Darboux transformations are key tools for solving such integrable models, providing insights into soliton interactions. Soliton gas emerges as a statistical ensemble in these systems, describing large numbers of solitons in a turbulent state. The Lax pair formalism ensures integrability, linking soliton dynamics to compatibility conditions in auxiliary systems. These systems find applications in Bose-Einstein condensates, nonlinear optics, and water waves, showcasing the interdisciplinary relevance of soliton gas. Theoretical advancements in integrable systems continue to deepen our understanding of soliton behavior and their collective dynamics in diverse physical contexts, bridging gaps between abstract mathematics and real-world phenomena.
10.2 Quantum Droplets and Soliton Dynamics
Quantum droplets, small clusters of atoms stabilized by quantum fluctuations, exhibit intriguing connections to soliton dynamics in the context of the Nonlinear Schrödinger Equation (NLSE). These droplets, related to Bose-Einstein condensates, form under specific conditions where quantum effects dominate, allowing for stable, localized wave-like structures. Soliton solutions of the NLSE provide a mathematical framework to describe the behavior of these droplets, including their formation, stability, and interactions. The concept of soliton gas, a statistical ensemble of solitons, offers insights into the collective behavior of numerous quantum droplets, modeling their dynamics and potential interactions. This interdisciplinary research bridges quantum physics with nonlinear optics and fluid dynamics, where solitons are also observed. By studying soliton dynamics in quantum droplets, researchers gain a deeper understanding of their behavior at the intersection of quantum mechanics and nonlinear wave phenomena, opening new avenues for theoretical and experimental exploration.
